Θεωρία της σχετικότητας: οι έννοιες

Πρόλογος

Ήταν γύρω στο 1900, όταν ο Kelvin διακήρυξε ότι «Η Φυσική έχει πια λύσει τα θεμελιακά προβλήματα. Από τώρα και μπρος δεν θα είναι παρά απλή εφαρμογή των γενικών νόμων. Μένουν βέβαια μερικά θεματάκια που δεν τα έχουμε κατανοήσει πλήρως: την κατανομή του μέλανος σώματος, οι φασματικές γραμμές των αερίων…». Δεν θα μπορούσε να φανταστεί, τότε, ότι τέτοια «θεματάκια» θα ανέτρεπαν, μέσα στα επόμενα χρόνια, εκ θεμελίων το πώς αντιλαμβανόμαστε τη φύση.

Η Φυσική ήταν πράγματι στις δόξες της στο τέλος του 19ου αιώνα. Ένα οικοδόμημα λιτό, κομψό και με μεγάλη εμβέλεια και βάθος ερμηνευτικής ισχύος. Η εξίσωση του Νεύτωνα (F=ma) καθόριζε την κίνηση υλικών σημείων και σωμάτων. Οι δυνάμεις F που προκαλούσαν την κίνηση ήταν, σε τελευταία ανάλυση, είτε βαρυτικές, είτε ηλεκτρομαγνητικές. Οι ηλεκτρομαγνητικές δυνάμεις διαδίδονταν με την ταχύτητα του φωτός, υπό μορφή κύματος και το φως ήταν μια ειδική περίπτωση διαδιδόμενου ηλεκτρομαγνητικού κύματος.
Η ύλη αποτελείτο από στοιχειώδη σωμάτια που συγκροτούνται μεταξύ τους λόγω αμοιβαίων ηλεκτρομαγνητικών δυνάμεων και οι ιδιότητες της ύλης μπορούσαν να ερμηνευτούν σαν αποτέλεσμα της μικροσκοπικής κίνησης των στοιχειωδών σωματιδίων.

Το μέλλον, λοιπόν, της φυσικής φάνταζε μάλλον μονότονο: Απλή εφαρμογή γνωστών κανόνων. Όμως κάτω από την επιφάνεια της πλήρους επιτυχίας, διαφαίνονταν κάποιες «ρωγμές» που σύντομα θα επέβαλαν την εκ βάθρων εννοιολογική αναδόμηση του κλασικού οικοδομήματος.

Σε αυτήν την εργασία προσεγγίζονται οι νέες έννοιες που εισήγαγε η θεωρία της σχετικότητας. Στον ιστότοπο αυτό μπορείτε να διαβάσετε και για τις νέες έννοιες που εισήγαγε και η κβαντομηχανική όσο και μια εισαγωγή στο όνειρο των φυσικών για την ανάπτυξη μιας ενιαίας θεωρίας των πάντων.

1) Η ειδική θεωρία της σχετικότητας

Το 1905 ο Einstein, βασιζόμενος στα νέα πειραματικά δεδομένα και υπερβαίνοντας τις κλασικές προκαταλήψεις, έφερε δύο νέες παραδοχές:

1. Η ταχύτητα του φωτός στο κενό είναι ίδια σε όλα τα συστήματα συντεταγμένων (Σ.Σ.) που βρίσκονται σε σχετική ομαλή κίνηση.

2. Όλοι οι νόμοι της φύσης είναι ίδιοι σε όλα τα Σ.Σ. που βρίσκονται σε σχετική ομαλή κίνηση.

Αυτές οι παραδοχές βρίσκονται σε αντίθεση με τους κλασικούς μετασχηματισμούς οι οποίοι πρέπει να αντικαταστούν. Τροποποιήσεις στις (1) και (2) οδηγούν σε αντίθεση με το πείραμα κι επομένως πρέπει να αποδεχτούμε την ισχύ τους και να αναθεωρήσουμε, τον τρόπο με τον οποίο μετασχηματίζονται οι θέσεις και οι ταχύτητες κατά τα πέρασμα από ένα Σ.Σ. σε άλλο. Σκοπός είναι να βγάλουμε συμπεράσματα από την (1) και (2), να δούμε πού και πώς αυτές οι παραδοχές έρχονται σε αντίθεση με τους κλασικούς μετασχηματισμούς, και να βρούμε τη φυσική σημασία των αποτελεσμάτων πού θα πετύχουμε.

Θα χρησιμοποιήσουμε το παράδειγμα ενός κινούμενου δωματίου με έναν εσωτερικό και έναν εξωτερικό παρατηρητή που κινείται κάθετα στους τοίχους. Αν εκπέμπεται ένα φωτεινό σήμα από το κέντρο του δωματίου, ρωτάμε τους δυο ανθρώπους τι περιμένουν να παρατηρήσουν, αν έχουν στο μυαλό τους μονάχα τις δυο αρχές.

Ο εσωτερικός παρατηρητής: Το φωτεινό σήμα που προχωρεί από το κέντρο του δωματίου θα φτάσει ταυτόχρονα στους δυο τοίχους, εφόσον απέχουν το ίδιο από τη φωτεινή πηγή και η ταχύτητα του φωτός είναι η ίδια προς όλες τις κατευθύνσεις.

Ο εξωτερικός παρατηρητής: Στο σύστημα μου η ταχύτητα του φωτός είναι ακριβώς η ίδια με την ταχύτητα στο σύστημα του παρατηρητή που κινείται με το δωμάτιο. Αυτό που βλέπω είναι ένα φωτεινό σήμα που διαδίδεται με μια σταθερή ταχύτητα, ίδια προς όλες τις κατευθύνσεις. Ο ένας τοίχος απομακρύνεται, από το φωτεινό σήμα, ο άλλος το πλησιάζει. Γι' αυτόν το λόγο, το φως θα συναντήσει λίγο πιο αργά τον τοίχο που απομακρύνε­ται, παρά τον τοίχο που πλησιάζει.

Συγκρίνοντας τις προβλέψεις των παρατηρητών μας, βρίσκουμε ένα συμπέρασμα που έρχεται σε αντίθεση με τις έννοιες της κλασικής φυσικής. Δυο γεγονότα, δηλ. οι δυο φωτεινές ακτίνες που χτυπούν τους δυο τοίχους, είναι σύγχρονα για τον εσωτερικό παρατηρητή, όχι όμως και για τον εξωτερικό. 
Στην κλασική φυσική είχαμε ένα ρολόι μο­νάχα, μια μοναδική ροή του χρόνου για όλους τους παρατηρητές, σε όλα Σ.Σ. Ο χρόνος, και κατά συνέπεια εκφράσεις όπως, «ταυτόχρονα», «νωρίτερα», «αργότερα», είχαν μια σημασία απόλυτα ανεξάρτητη από οποιοδήποτε Σ.Σ.

Η θεωρία της σχετικότητας μας υποχρεώνει να εγκαταλείψουμε αυτή την άποψη. Και πρέπει να κατανοήσουμε τη σημασία της πρότασης: «Δυο γεγονότα πού είναι σύγχρονα σε ένα Σ.Σ., μπορεί να μην είναι σύγχρονα σε ένα άλλο Σ.Σ.». Πριν από αυτό, όμως, πρέπει να εξηγήσουμε τι εννοούμε με το «δυο γεγονότα σύγχρονα σε ένα Σ.Σ.».

Για να συζητήσουμε αυτά χρειαζόμαστε ρολόγια. Οποιοδήποτε φυσικό φαινόμενο μπορεί να χρησιμέψει για ρολόι, φτάνει να επαναλαμβάνεται με ακρίβεια όσες φορές θελήσουμε.

Ας θεωρήσουμε πως σε δυο σημεία που απέχουν μεταξύ τους, έχουμε τοποθετήσει δυο τέλεια ρολόγια, που δείχνουν ακριβώς την ίδια ώρα. Πώς μπορούμε να είμαστε βέβαιοι, πως δυο απομακρυσμένα ρολό­για δείχνουν ακριβώς την ίδια ώρα; Θα μπορούσαμε να τοποθετηθούμε σ' ένα σημείο πού να απέχει το ίδιο κι από τα δυο ρολόγια, και να παρατηρούμε σ' αυτό το σημείο τα είδωλα τους πού μεταδίδονται από μια τηλεόραση που ισαπέχει από τα δύο. Αν τα δυο σήματα εκπέμπονται ταυτόχρονα, θα φτάσουνε σε μένα την ίδια στιγμή. Αν δυο «καλά» ρολόγια πού παρατηρούνται από τη μέση της απόστασης πού τα χωρίζει δεί­χνουν πάντα την ίδια ώρα, τότε είναι κατάλληλα για να δείχνουν την ώρα σε δυο σημεία απομακρυσμένα μεταξύ τους.

Ωστόσο το να χρησιμοποιούμε μονάχα ένα ρολόι δεν μας εξυπηρετεί, γιατί είμαστε υποχρεωμένοι να κάνουμε όλες μας τις μετρήσεις κοντά του. Παρατηρώντας από μακριά το ρολόι, π.χ. μέσω της τηλεόρασης, πρέπει πάντα να 'χουμε στο μυαλό μας, πώς εκείνο πού βλέπουμε τώρα, έγινε στην πραγματικότητα πρωτύτερα. Είμαστε υποχρεωμένοι να κάνουμε διορθώσεις σ' όλες μας τις χρονικές μετρήσεις, ανάλογα με την απόσταση μας από το ρολόι.

Δε βολεύει λοιπόν να έχουμε μονάχα ένα ρολόι. Αλλά μια και ξέρουμε τώρα πώς να ξεκαθαρίσουμε αν δυο ή περισσότερα ρολόγια δείχνουν την ίδια ώρα και δουλεύουν με τον ίδιο ρυθμό, μπορούμε να φανταστούμε όσα ρολόγια θέλουμε μέσα σ' ένα δοσμένο Σ.Σ. Καθένα τους θα μας βοηθά να καθορίζουμε το χρόνο των γεγονότων πού συμβαίνουν στην άμεση γειτονιά του. Όλα τα ρολόγια ηρεμούν σε σχέση με το Σ.Σ. Είναι «καλά» και συγχρονισμέναρολόγια, που σημαίνει πώς δείχνουν την ίδια ώρα. 
Τα γεγονότα είναι σύγχρονα αν τα συγχρονισμένα ρολόγια που βρίσκονται κοντά τους, δείχνουν την ίδια ώρα, τη στιγμή που παράγονται. Το να λέμε πως ένα από τα απομακρυσμένα γεγονότα συνέβη πριν από το άλλο, έχει τώρα καθορισμένο νόημα.

Για να διαπραγματευθούμε το πρόβλημα δυο συστημάτων που βρίσκονται σε σχετική ομαλή κίνηση, πρέπει να θεωρήσουμε δυο ράβδους, εφοδιασμένες με ρολόγια. Ο παρατηρητής σε καθένα απ' αυτά τα δυο Σ.Σ., έχει τώρα τη δική του ράβδο και τη δική του σειρά ρολογιών σταθερά δεμένων μ' αυτήν.

Όταν διαπραγματευτήκαμε το ζήτημα των μετρήσεων στην κλασική μηχανική, χρησιμοποιήσαμε μονάχα ένα ρολόι, για όλα τα Σ.Σ. Εδώ έχουμε πολλά ρολόγια για κάθε Σ.Σ. Η διαφορά αυτή δεν έχει σημασία. Ωστόσο κανείς δε μπορεί να έχει αντίρρηση (για λόγους ευκολίας) στη χρησιμοποίηση των πολλών, φτά­νει να συμπεριφέρνονται σαν καλά συγχρονισμένα ρολόγια.

Τώρα πλησιάζουμε τo σημείο που φανερώνει πού έρχονται σε αντίθεση οι κλασικοί μετασχηματισμοί με τη θεωρία της σχετικότητας. Τι συμβαίνει όταν δυο σειρές ρολόγια κινούνται ομαλά, η μια σε σχέση με την άλλη; Ο κλασικός φυσικός θα απαντούσε: τίποτα.

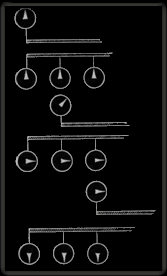
Ωστόσο θα μπορούσαμε να φανταστούμε κι ένα κινούμενο ρολόι που προχωρεί με διαφορετικό ρυθμό από ένα ακίνητο. Ας συζητήσουμε αυτή τη δυνατότητα. Τι εννοούμε λέγοντας πως ένα ρολόι που κινείται αλλάζει ρυθμό; Ας δεχτούμε, για λόγους απλότητας, πως έχουμε μονάχα ένα ρολόι στο επάνω Σ.Σ. και πολλά στο κάτω. Όλα τα ρολόγια έχουν τον ίδιο μηχανισμό και τα κάτω είναι συγχρονισμένα. Σχεδιάσαμε τρεις διαδοχικές θέσεις των δυο Σ.Σ. πού κινούνται ομαλά το ένα σε σχέση με το άλλο. Στο πρώτο σχήμα, οι δείκτες του επάνω και των κάτω ρολογιών βρίσκονται στην ίδια θέση, γιατί έτσι τους βάλαμε. Όλα τα ρολόγια δείχνουν την ίδια ώρα. Στο δεύτερο σχέδιο βλέπουμε τις σχετικές θέσεις των δυο Σ.Σ. υστέρα από κάποιο χρόνο. 
Όλα τα ρολόγια στο κάτω Σ.Σ. δείχνουν ιδίαν ώρα, αλλά το ρολόι στο επάνω Σ.Σ. δεν προχωρεί πια με τον ίδιο ρυθμό. Ο ρυθμός άλλαξε και η ώρα είναι διαφορετική, γιατί το ρολόι κινείται σχε­τικά με το κάτω Σ.Σ. Στο τρίτο σχήμα, βλέπουμε πώς η διαφορά των θέσεων των δεικτών αυξάνει με τον χρόνο. 
Ένας παρατηρητής που βρίσκεται ακίνητος στο κάτω Σ.Σ. θα ‘βρισκε πως ένα ρολόι που κινείται, μεταβάλλει ρυθμό. Στο ίδιο αποτέλεσμα θα έφτανε κανείς αν το ρολόι κινιότανε σχετικά μ' ένα παρατηρητή ακίνητο στο πάνω Σ.Σ. Σ' αυτή την περίπτωση θα 'πρεπε να υπάρχουν πολλά ρολόγια στο πάνω Σ.Σ., και ένα μονάχα στα κάτω. Οι νόμοι της φύσης πρέπει να είναι ίδιοι στα δυο Σ.Σ. 
Στην κλασική μηχανική, λοιπόν, γινόταν δεκτό σιωπηρά, πως ένα κινούμενο ρολόι δεν αλλάζει το ρυθμό του. Ωστόσο μπορούμε να φανταστούμε πως ένα κινούμενο ρολόι μεταβάλλει ρυθμό, εφόσον ο νόμος αυτής της αλλαγής είναι ο ίδιος για όλα τα συστήματα αδράνειας.

Ας μελετήσουμε τώρα και το μήκος. Ας πάρουμε μια ράβδο με μήκος ένα μέτρο. Αυτό σημαίνει πως έχει μήκος ένα μέτρο, εφ' όσον ηρεμεί σε ένα Σ.Σ. Ας υποθέσουμε τώρα πως κινείται ομαλά, γλιστρώντας κατά μήκος της ράβδου που αντιπροσωπεύει το Σ.Σ. Το μήκος της θα φαίνεται ότι είναι πάντα ένα μέτρο; Πρώτα πρέπει να ξέρουμε πώς να προσδιορίσουμε το μήκος της όταν βρίσκεται σε κίνηση. Αυτό μπορεί να γίνει με τον ακόλουθο τρόπο: Σε μια δοσμένη στιγμή, δυο παρατηρητές φωτογραφίζουν ταυτόχρονα, ο ένας την αρχή κι ο άλλος το τέλος της. Αφού οι εικόνες πάρθηκαν ταυτόχρονα, μπορούμε να συγκρίνουμε πάνω στη ράβδο που παριστάνει το Σ.Σ., τα σημάδια με τα οποία συμπίπτουν η αρχή και το τέλος της ράβδου. 
Χρειαζόμαστε δυο παρατηρητές για να σημειώσουν σύγχρονα γεγονότα σε διαφορετικές θέσεις ενός δοσμένου Σ.Σ. Αφού οι φωτογραφίες πρέπει να παρθούν ταυτόχρονα και το «ταυτόχρονα» είναι μια σχετική έννοια πού εξαρτάται από το Σ.Σ., φαίνεται δυνατό να είναι διαφορετικά τα αποτελέσματα αυτών των μετρήσεων, σε διαφορετικά Σ.Σ. πού βρίσκονται σε σχετική κίνηση.

Γνωρίζουμε ότι η ταχύτητα του φωτός, είναι ίδια σ' όλα τα συστήματα αδράνειας. Είναι αδύνατο να συμφιλιώσουμε το γεγονός αυτό, με τους κλασικούς μετασχηματισμούς. Ο κύκλος των παραδοχών μας πρέπει να σπάσει σε κάποιο σημείο. Μήπως αυτό μπορεί να γίνει σε τούτο ακριβώς το σημείο; Μήπως δηλαδή μπορούμε να δεχτούμε αλλαγές στο ρυθμό του κινούμενου ρολογιού και στο μήκος της κινούμενης ράβδου, τέτοιες ώστε η σταθερότητα της ταχύτητας του φωτός να είναι άμεσο επακόλουθο τους; 
Το επιχείρημα μπορεί και να αντιστραφεί: αν η ταχύτητα του φωτάς είναι ίδια σ' όλα τα Σ.Σ., τότε κινούμε­νες ράβδοι πρέπει να μεταβάλλουν τα μήκη τους και κινούμενα ρολό­για πρέπει να μεταβάλλουν το ρυθμό τους.

Αυτά μπορεί να φαίνονται περίεργα, αλλά από τη σκοπιά της θεωρίας της σχετικότητας, οι αντιλήψεις της κλασικής φυσικής φαίνονται αυθαίρετες. Γιατί να πιστεύουμε στον απόλυτο χρόνο, που ρέει με τον ίδιο τρόπο για όλους τους παρατηρητές, σε όλα τα Σ.Σ.; Γιατί να πιστεύουμε πως η απόσταση είναι αμετάβλητη; Οχρόνος καθορίζεται από ρολόγια, οι συντεταγμένες του χώρου από ράβδους και το αποτέλεσμα του καθορισμού τους εξαρ­τάται από τη συμπεριφορά αυτών των ρολογιών και των ράβδων, όταν βρίσκονται σε κίνηση.

Άλλωστε οι εξισώσεις Maxwell δεν είναι αναλλοίωτες σε σχέση με τους κλασικούς μετασχηματισμούς. Αυτό υποδεικνύει πως η σύνδεση ανάμεσα σε δυο Σ.Σ. πρέπει να είναι διαφορετική. Απεναντίας, οι εξισώσεις Maxwell, είναι αναλλοίωτες σε σχέση με τους μετασχηματισμούς Lorentz οι οποίοι περιλαμβάνουν και νόμους μετασχηματισμού για το χρόνο. Στην κλασική φυσική είχαμε νόμους μετασχηματισμού για τις συντεταγμένες και για τις ταχύτητες, αλλά οι νόμοι της μηχανικής ήταν ίδιοι για δυο Σ.Σ. που βρισκότανε σε σχετική ομαλή κίνηση. Είχαμε νόμους μετασχηματισμού για το χώρο, όχι όμως και για το χρόνο, γιατί ο χρόνος ήταν ο ίδιος για όλα τα Σ.Σ. Τα πράγματα είναι διαφορετικά στη θεωρία της σχετικότητας: Έχουμε νόμους μετασχηματισμού για το χώρο, το χρόνο και την ταχύτητα, διαφορετικούς από της κλασικής μηχανι­κής. 
Και πάλι, οι  νόμοι της φύσης πρέπει να είναι ίδιοι για όλα τα Σ.Σ. πού βρίσκονται σε ομαλή σχετική κίνηση. Σ' όλα τα συστήματα αδράνειας ισχύουν οι ίδιοι νόμοι και το πέρασμα από το ένα στο άλλο γίνεται με τους μετασχηματισμούς του Lorentz.

Από αυτούς συνάγεται πως μια κινούμενη ράβδος συστέλλεται προς την κατεύθυνση της κίνησης και η συστολή μεγαλώνει με την αύξηση της ταχύτητας. Δεν υπάρχει όμως συστολή κατά τη διεύθυνση που είναι κάθετη με τη διεύθυνση της κίνησης. Το μήκος μιας ράβδου θα 'φτάνε στο μηδέν, αν η ταχύτητα της έφτανε την ταχύτητα του φωτός. Επίσης ο ρυθμός ενός κινούμενου ρολογιού θα επιβραδυνότανε σε σύγκριση με των ρολογιών μπροστά από τα όποια περνά και θα μηδενιζόταν, αν το ρολόι έφτανε να κινείται με την ταχύτητα του φωτός. Ο αριθμός που εκφράζει την ταχύτητα του φωτός εμφανίζεται στους μετασχηματισμούς του Lorentz και παίζει το ρόλο οριακής ταχύτητας, όπως η άπειρη ταχύτητα στην κλασική μηχανική.

2) Ειδική σχετικότητα και μηχανική

Δεν ήταν δύσκολο να τροποποιήσουμε την κλασική μηχανική έτσι, ώστε να μην έρχεται σε αντίθεση με τη θεωρία της σχετικότητας. Η παλιά μηχανική ισχύει για μικρές ταχύτητες και αποτελεί την οριακή περίπτωση της νέας. 
Ας δούμε ένα παράδειγμα αλλαγής που εισάχθηκε από τη θεωρία της σχετικότητας.

Ας φανταστούμε ένα σώμα ορισμένης μάζας, που κινείται κατά μήκος μιας ευθείας γραμμής και υφίσταται τη δράση μιας εξωτερικής δύναμης κατά την κατεύθυνση της κίνησης του. Για την κλασική μηχανική, δύναμη είναι ανάλογη με την αλλαγή της ταχύτητας. Για την θεωρία της σχετικότητας, ο νόμος αυτός ισχύει προσεγγιστικά και μόνο για μικρές ταχύτητες. Για αυτήν, όσο πιο πολύ πλησιάζει μια ταχύτητα την ταχύτητα του φωτάς, τόσο πιο δύσκολο είναι να αυξηθεί. Κι όταν μια ταχύτητα είναι ίση με του φωτάς, είναι αδύνατο να την αυξήσουμε περισσότερο.

Ένα ακίνητο σώμα έχει ορισμένη μάζα, που ονομάζεται μάζα ηρεμίας. Ένα σώμα αντιπαρατάσσει στην αλλαγή της ταχύτητας μεγαλύτερη αντίσταση, όχι μόνο αν η μάζα ηρεμίας του είναι μεγαλύτερη, αλλά κι αν η ταχύτητα του είναι μεγαλύτερη και γίνεται απείρως μεγάλη, όταν η ταχύτητα πλησιάζει την ταχύτητα του φωτός.

Το αποτέλεσμα αυτό υποβάλλει μιαν άλλη σπουδαία γενίκευση. Ένα σώμα σε ηρεμία έχει μάζα, όχι όμως και κινητική ενέργεια. Ένα κινούμενο σώμα έχει και μάζα και κινητική ενέργεια. Το σώμα αυτό αντιστέκεται στην αλλαγή της ταχύτητας, ισχυρότερα από το ακίνητο σώμα. Θα 'λέγε κανείς πώς η κινητική ενέργεια του κινούμενου σώματος, αυξάνει την αντίσταση του. Αν δυο σώματα έχουν την ίδια μάζα, αυτό που έχει μεγαλύτερη κινητική ενέργεια, αντιστέκεται πιο έντονα στη δράση μιας εξωτερικής δύναμης. 
Ας φανταστούμε ένα κουτί που περιέχει σφαίρες και ηρεμεί, τόσο αυτό, όσο κι οι σφαίρες, στο Σ.Σ. του. Για να το κινήσουμε, για να το επιταχύνουμε, χρειάζεται κάποια δύναμη. Άραγε αυτή η ίδια δύναμη θα προκαλέσει την ίδια επιτάχυνση, αν οι σφαίρες κινούνται μέσα στο κουτί προς όλες τις διευθύνσεις με μέση ταχύτητα που πλησιάζει την ταχύτητα του φωτός; Όχι. Θα χρειαστεί μια μεγαλύτερη δύναμη, εξ αιτίας της αυξημένης κινητικής ενέργειας των σφαιρών, η οποία αυξάνει την αντίσταση του κουτιού. Η κινη­τική ενέργεια λοιπόν, αντιστέκεται στην κίνηση, όπως ακριβώς και οι ζυγίσιμες μάζες. Ισχύει άραγε το ίδιο για όλα τα είδη της ενέργειας;

Η θεωρία της σχετικότητας συνάγει, λοιπόν, από τη θεμελιώδη της παραδοχή ότι κάθε ενέρ­γεια αντιστέκεται στην αλλαγή της κίνησης. Κάθε ενέργεια συμπεριφέρεται όπως η ύλη. 
Σύμφωνα με τη θεωρία της σχετικότητας δεν υπάρχει ουσιώδης διάκριση ανάμεσα στη μάζα και την ενέργεια. Η ενέργεια έχει μάζα και η μάζα αντιπροσωπεύει ενέργεια. Κι αντί για δυο νόμους διατήρησης (ενέργειας και μάζας), έχουμε ένα μονάχα, το νόμο για τη μάζα-ενέργεια.

Ο λόγος για την έλλειψη άμεσης εμπειρίας αυτών, είναι η εξαιρετικά μικρή σχέση αναλογίας ανάμεσα στη μάζα και την ενέργεια. Η ποσότητα της θερμότητας πού μπορεί να μετατρέψει τριάντα χιλιάδες τόνους νερού, σε ατμό, θα ζύγιζε ένα γραμμάριο περίπου δεδομένου ότι ισχύει η περίφημη εξίσωση:

όπου c η ταχύτητα του φωτός.

3) Ο χωρόχρονος

Μέχρι τώρα εξετάσαμε μόνο ευθύγραμμες κινήσεις. Το Σ.Σ. μας ήταν μια σταθερή ράβδος που είχε αρχή και δεν είχε τέλος. Θα διατηρήσουμε αυτό τον περιορισμό και θα πάρουμε διάφορα σημεία πάνω στη ράβδο: Οι θέσεις τους μπορούν να καθοριστούν από την τετμημένη του σημείου κι αντίθετα, σε κάθε τετμημένη αντιστοιχεί το αντίστοιχο σημείο πάνω στη ράβδο.

Αυτό εκφράζεται με την πρόταση: όλα τα σημεία πάνω στη ράβδο, αποτελούν ένα μονοδιάστατο συνεχές. Η αυθαίρετη μικρότητα των βημάτων που συνδέουν δυο απομακρυσμένα σημεία, είναι χαρακτηριστικό του συνεχούς. Ένα επίπεδο είναι ένα δισδιάστατο συνεχές ενώ ο χώρος είναι ένα τρισδιάστατο συνεχές.

Για να επιστρέψουμε στη φυσική, πρέπει να θεωρήσουμε την κίνηση υλικών σωματιδίων. Για να παρατηρήσουμε και να προβλέψουμε φυσικά φαινόμενα, πρέπει να λάβουμε υπ' όψη μας όχι μονάχα τη θέση, αλλά και τα χρόνο στον οποίο πραγματοποιούνται.

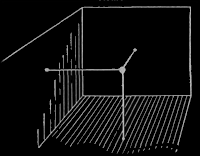
Ας πάρουμε το παράδειγμα της ελεύθερης πτώσης ενός σώματος. Η πτώση σ' ένα μονοδιάστατο χώρο, παριστάνεται εδώ από μια καμπύλη σ' ένα δισδιάστατο χωροχρονικό συνεχές. Σε κάθε σημείο του χωροχρονικού μας συνεχούς αντιστοιχεί ένα ζευγάρι αριθμών, από τους οποίους ο ένας δηλώνει την συντεταγμένη του χρόνου και ο άλλος τη συντεταγμένη του χώρου. Αντίστροφα: ένα ορισμένο σημείο στο χωροχρονικό μας επίπεδο, αντιστοιχεί σε κάθε ζευγάρι αριθμών πού χαρακτηρίζουν ένα γεγονός. Δυο γειτονικά σημεία αντιπροσωπεύουν δυο γεγονότα πού έγιναν σε θέσεις και σε χρόνους ελαφρά διαφορετικούς. (Με αυτά δεν ενώνουμε τον χώρο με τον χρόνο. Απλά χρησιμοποιούμε μια δυναμική παράσταση όπου οι θέσεις αλλάζουν με το χρόνο).

Μπορούμε ωστόσο την ίδια κίνηση να την παραστήσουμε με διαφορετικά τρόπο. Μπορούμε να κάνουμε μια στατικήπαράσταση, θεωρώντας την καμπύλη σ’ ένα δισδιάστατο χωροχρονικά συνεχές. Η κίνηση παριστάνεται τώρα σαν κάτι που είναι, που υπάρχει σε ένα δισδιάστατο χωροχρονικό συνεχές, και όχι σαν κάτι που μεταβάλλεται σ' ένα μονοδιάστατο χωρικό συνεχές.

Οι δυο αυτές παραστάσεις είναι αυστηρά ισοδύναμες και είναι ζήτημα σύμβασης να προτιμάμε τη μια από την άλλη.

Τίποτα απ' όσα ειπώθηκαν εδώ για τις δυο παραστάσεις της κίνησης, δεν έχει σχέση με τη θεωρία της σχετικότητας. Οι δυο παραστάσεις μπορούν να χρησιμοποιούνται ισοδύναμα, αν και η κλασική φυσική προτιμούσε κυρίως τη δυναμική παράσταση, περιγράφοντας την κίνηση σαν σειρά γεγονότων στο χώρο και όχι στο χωροχρόνο. Αλλά η θεωρία της σχετικότητας, άλλαξε αυτή τη σκοπιά. Είναι σαφώς υπέρ της στατικής εικόνας και βρήκε σε τούτη την παράσταση της κίνησης μια πιο αντικειμενική εικόνα της πραγμα­τικότητας. Αλλά γιατί αυτές οι δυο παραστάσεις, που από την κλασική σκοπιά είναι ισο­δύναμες, δεν είναι κι από την άποψη της θεωρίας της σχετικότητας;

Θα μπορέσουμε να απαντήσουμε, αν ξαναδούμε δυο Σ.Σ. με ομαλή σχετική κίνηση.

Σύμφωνα με την κλασική φυσική, παρατηρητές σε δυο Σ.Σ. με σχετική ομαλή κίνηση, θα αποδώσουν σε ένα καθορισμένο γεγονός διαφορετικές συντεταγμένες του χώρου, αλλά την ίδια χρονική συντεταγμένη. Στο παράδειγμα της ελεύθερης πτώσης, η σύμπτωση του σωματιδίου με το έδαφος χαρακτηρίζεται στο Σ.Σ. που εκλέξαμε από τη συντεταγμένη του χρόνου «4» και τη συντεταγμένη του χώρου «μηδέν». Σύμφωνα με την κλασική μηχανική, το χαλίκι θα φτάσει το έδαφος ύστερα από τέσσερα δευτερόλεπτα και για έναν παρατηρητή με ομαλή κίνηση ως προς το Σ.Σ. πού εκλέξαμε. Αυτός ο παρατηρητής θα αναφέρει ωστόσο την απόσταση στο Σ.Σ. του, και θα αποδώσει γενικά διαφορετικές χωρικές συντεταγμένες στα γεγονός της κρούσης. Για κάθε Σ.Σ., το δισδιάστατο συνεχές μπορεί να χωριστεί σε δυο μονοδιάστατα συνεχή: χρόνο και χώρο.

Σύμφωνα με τη θεωρία της σχετικότητας, όμως,  ο χρόνος που το χα­λίκι θα αγγίξει τη γη, δεν θα είναι ο ίδιος για όλους τους παρατηρητές. Η συντεταγμένη του χρόνου και η συντεταγμένη του χώρου θα είναι διαφορετικές σε δυο διαφορετικά Σ.Σ. και η μεταβολή στη συντεταγμένη του χρόνου θα είναι πολύ έντονη, αν η σχετική ταχύτητα πλησιάζει την ταχύτητα του φωτός. Το δισδιάστατο συνεχές δε μπορεί να χωριστεί σε δυο μονοδιάστατα, όπως στην κλασική φυσική. Δεν πρέπει να εξετάζουμε τα χώρο και το χρόνο χω­ριστά, όταν καθορίζουμε τις χωροχρονικές συντεταγμένες σε  ένα άλλο Σ.Σ. Ο χωρισμός του δισδιάστατου συνεχούς σε δυο μονοδιάστατα, είναι αυθαίρετος και δεν έχει αντικειμενικό νόημα.

Είναι εύκολο να επεκτείνουμε όσα είπαμε, στην περίπτωση που η κίνηση γίνεται σε τρεις χωρικές διαστάσεις. Η χρονική στιγμή ενός γεγονότος είναι ο τέταρτος αριθμός. Σε κάθε γεγονός αντιστοιχούν τέσσερις ορισμένοι αριθμοί κι αντίστροφα ένα ορισμένο γεγονός, αντιστοιχεί σε τέσσερις αριθμούς. Έτσι κόσμος των γεγονότων, αποτελεί ένα τετραδιάστατο συνεχές. Η τελευταία πρόταση είναι αληθινή για την κλασική φυσική, όσο και για τη θεωρία της σχετικότητας. Η διαφορά παρουσιάζεται όταν μελετούμε δυο Σ.Σ. με σχετική κίνηση. Το δωμάτιο κινείται, και ο εσωτερικός και εξωτερικός παρατηρητής προσδιορίζουν τις χωροχρονικές συντεταγμένες των ίδιων γεγονότων. Ο κλασικός φυσικός χωρίζει πάλι το τετραδιάστατο συνεχές, σε τρισδιάστατο χωρικό συνεχές και το μονοδιάστατο χρονικό. Αλλά κατά τη θεωρία της σχετικότητας, τόσο ο χρόνος όσο κι ο χώρος μεταβάλλονται όταν περνά κανείς από ένα Σ.Σ. σε άλλο. Οι μετασχηματισμοί του Lorentz καθορίζουν τις ιδιότητες μετασχηματισμού του τετραδιάστατου κόσμου των γεγονότων.

Ο κόσμος των γεγονότων μπορεί να περιγραφεί δυναμικά με μια εικόνα που μεταβάλλεται με το χρόνο και που προβάλλεται στο φόντο του τρισδιάστατου χώρου. Αλλά μπορεί να περιγραφεί και με μια στατική εικόνα, στο φόντο του τετραδιάστατου χωροχρονικού συνεχούς. Από την άποψη της κλασικής φυσικής, οι δυο εικόνες, δυναμική και στατική, είναι ισοδύναμες. Από την άποψη της θεωρίας της σχετικότητας, ή στατική εικόνα είναι πιο βολική και πιο αντικειμενική.

Ακόμα και στη θεωρία της σχετικότητας μπορούμε, αν το προτιμάμε, να χρησιμοποιούμε τη δυναμική εικόνα. Αλλά πρέπει να θυμόμαστε πως ο χωρισμός αυτός σε χώρο και χρόνο δεν έχει αντικειμενικό νόημα, μια και ο χρόνος δεν είναι πια «απόλυτος». Ωστόσο, στα παρακάτω θα χρησιμοποιούμε πάντα τη «δυναμική» και όχι τη «στατική» γλώσσα.

4) Η γενική θεωρία της σχετικότητας

Κάνοντας μια εισαγωγή στη γενική θεωρία της σχετικότητας, θα προσπαθήσουμε να απαντήσαμε πρώτα σ' ένα θεμελιώδες ερωτήματα: Υπάρχει σύστημα αδράνειας; Μάθαμε κάτι για τους νόμους της φύσης, την αμεταβλητότητά τους ως προς τους μετασχηματισμούς του Lorentz και την ισχύ τους για τα συστήματα αδράνειας που κινούνται ομαλά το ένα ως προς το άλλο. Αλλά ποιο είναι το πλαίσιο στο οποίο πρέπει να τους αναφέρουμε;

Για να καταλάβουμε καλύτερα τη δυσκολία που εμφανίζεται, θέσουμε λίγες απλές ερωτήσεις: Τι είναι σύστημα αδράνειας; Ο κλασικός φυσικός θα απαντούσε: «Είναι ένα Σ.Σ. οπού ισχύουν οι νόμοι της μηχανικής. Ένα σώμα πού πάνω του δε δρα εξωτερική δύναμη, κινείται ομαλά μέσα σε ένα τέτοιο Σ.Σ. Αυτή η ιδιότητα μας κάνει λοιπόν ικανούς να διακρίνουμε ένα σύστημα αδράνειας, από οποιοδήποτε άλλο». Ωστόσο, τι εννοεί όταν λέει πως στο σώμα δε δρα καμιά δύναμη; Ο φυσικός μας θα αναγκαζόταν να ομολογήσει: «Εννοώ απλώς ότι το σώμα κινείται ομαλά σε ένα σύστημα αδράνειας». Βρισκόμαστε  μπροστά στην  αρχική  μας ερώτηση… Και τι είναι σύστημα αδράνειας;

Αυτή είναι μια σοβαρή δυσκολία στην κλασική φυσική. Έχουμε νόμους, αλλά δεν ξέρουμε σε ποιο πλαίσιο να τους αναφέρουμε.

Μπορούμε να πλησιάσουμε την ίδια δυσκολία από μια διαφορετική οπτική. Ας υποθέσουμε πως σ' ολόκληρο το σύμπαν υπάρχει μόνο ένα σώμα, που αποτελεί τα Σ.Σ. μας. Το σώμα αυτό αρχίζει να περιστρέφεται. Σύμφωνα με την κλασική μηχανική, οι νόμοι της φυσικής για ένα περιστρεφόμενο σώμα, είναι διαφορετικοί από τους νόμους για ένα σώμα που δεν περιστρέφεται. Αν η αρχή της αδράνειας ισχύει στη μια περί­πτωση, δεν ισχύει στην άλλη. Όλα αυτά όμως φαίνονται πολύ ύποπτα. Μας επιτρέπεται να θεωρούμε την κίνηση ενός μονάχα σώματος, μέσα σ' όλο το σύμπαν; Λέγοντας κίνηση ενός σώματος, εννοούμε πάντα την αλλαγή της θέσης του ως προς ένα άλλο σώμα. Είναι λογικό να μιλάμε για κίνηση ενός μοναχικού σώματος; Η κλασική μηχανική και η κοινή λογική βρίσκονται σε ασυμφωνία σ' αυτό το σημείο. Ο κανόνας του Νεύτωνα είναι: αν ισχύει η αρχή της αδράνειας, τότε το Σ.Σ. βρίσκεται είτε σε ηρεμία, είτε σε ομαλή κίνηση. Αν ή αρχή της αδράνειας δεν ισχύει, τότε το κινούμενο σώμα βρίσκεται σε μεταβαλλόμενη κίνηση.

Στην κλασική φυσική δεν υπάρχει απόλυτη ομαλή κίνηση. Αν δυο συστήματα συντεταγμένων κινούνται ομαλά μεταξύ τους, δεν έχει νόημα να πούμε: «Τούτο τα Σ.Σ. ηρεμεί και το άλλο κινείται». Αλλά αν δυο Σ.Σ. κινούνται ανομοιόμορφα το ένα ως προς το άλλο, τότε έχει νόημα να πούμε: «Αυτό το σώμα κινείται, και το άλλο ηρεμεί (ή κινείται ομαλά)». Η απόλυτη κίνηση έχει εδώ καθορισμένο νόημα. Οι δυσκολίες πού αναφέραμε, δηλαδή οι δυσκολίες του συστήματος αδράνειας και της απόλυτης κίνησης, είναι στενά δεμένες μεταξύ τους. Η απόλυτη κίνηση γίνεται δυνατή μόνο με την ιδέα ενός συστήματος αδράνειας, για το οποίο ισχύουν οι νόμοι της φύσης.

Θα έτεινε κανείς να πιστέψει πως δεν υπάρχει διέξοδος απ' αυτές τις δυσκολίες. Η ρίζα τους βρίσκεται στo ότι οι νόμοι της φύσης ισχύουν μόνο για μια ειδική τάξη Σ.Σ., δηλαδή για τα συστήματα αδράνειας. Η δυνατότητα να ξεπεραστούν οι δυσκολίες, εξαρτάται από την απάντηση που δίνει κανείς στην ερώτηση: Μπορούμε να διατυπώσουμε τους νόμους της φυσικής με τέτοιο τρόπο, ώστε να ισχύουν για όλα τα Σ.Σ., δηλαδή όχι μονάχα για κείνα που κινούνται ομαλά, αλλά και για κείνα πού κινούνται με οποιοδήποτε τρόπο μεταξύ τους; Αν αυτό μπορεί να γίνει, οι δυσκολίες μας θα ξεπεραστούν.

Τελικά αποδείχθηκε πως μπορούμε να δημιουργήσουμε μια φυσική στηριγμένη στη σχετικότητα πού να ισχύει για όλα τα Σ.Σ., μια φυσική οπού δε θα υπάρχει θέση για την απόλυτη, αλλά μονάχα για τη σχετική κίνηση.

Έχουμε μια τουλάχιστον ένδειξη, για το πώς μπορεί κανείς να οικοδομήσει τη νέα φυσική. Η πραγμα­τική σχετικιστική φυσική πρέπει να ισχύει σε όλα τα Σ.Σ. και κατά συνέπεια και στην ειδική περίπτωση του συστήματος αδράνειας. Γνωρίζουμε ήδη τους νόμους για το τελευταίο. Οι νέοι γενικοί νόμοι, πού θα ισχύουν για όλα τα Σ.Σ., πρέπει να ανάγονται στους παλιούς γνωστούς νόμους, στην ειδική περίπτωση του συστήματος αδράνειας.

Το πρόβλημα να διατυπωθούν οι νόμοι της φυσικής για οποιοδήποτε Σ.Σ., λύθηκε από τη γενική θεωρία της σχετικότητας. Η ειδική θεωρία της σχετικότητας εφαρμόζεται μονάχα σε συστήματα αδράνειας. Οι δυο θεωρίες δε μπορούν να έρχονται σε αντίθεση, γιατί πρέπει πάντα να συμπεριλαμβάνουμε τους παλιούς νόμους της ειδικής θεωρίας της σχετικότητας, στους γενικούς νόμους για ένα σύστημα αδράνειας. Απλά το σύστημα αδράνειας, για το όποιο διατυπώθηκαν αρχικά οι νόμοι της φυσικής, δεν αποτελεί τώρα παρά μια οριακή ειδική περίπτωση.

Αλλά σκιαγραφώντας το δρόμο που ακολουθήθηκε για την πραγματοποίηση της νέας θεωρίας, θα αναγκαστούμε να είμαστε πιο ασαφείς απ' ότι ως τώρα. Νέες δυσκολίες που προβάλλουν στην ανάπτυξη της επιστήμης, υποχρεώνουν τη θεωρία να γίνεται όλο και πιο αφηρημένη. Γιατί όσο πιο απλές και θεμελιώδεις γίνονται οι παραδοχές μας, τόσο γίνεται πιο περίπλοκο το μαθηματικό όργανο σκέψης.

Η νέα ιδέα είναι απλή: να δημιουργήσουμε μια φυσική πού να ισχύει για όλα τα Σ.Σ. Η πραγματοποίηση της συνεπιφέρει περιπλοκές στη μαθηματική διατύπωση και μας υποχρεώνει να χρησιμοποιήσουμε διαφορετικά μαθηματικά όργανα. Εδώ θα δείξουμε μονάχα τη σύνδεση ανάμεσα στην πραγματοποίηση αυτού του προγράμματος και σε δυο βασικά προβλήματα: τη βαρύτητα και τη γεωμετρία.

5) Η νέα αντίληψη για τα «μη αδρανειακά» συστήματα

Ας φανταστούμε ένα μεγάλο ανελκυστήρα, στο τελευταίο πάτωμα ένας ουρανοξύστη. Το συρματόσκοινο που κρατάει τον ανελκυστήρα σπάει κι ο ανελκυστήρας αρχίζει να πέφτει ελεύθερα. Παρατηρητές μέσα στον ανελκυστήρα, κάνουν πειράματα στη διάρκεια της πτώσης σε ιδεώδεις συνθήκες. Ένας από τους παρατηρητές βγάζει από την τσέπη του ένα μαντήλι και ένα ρολόι και τα αφήνει ελεύθερα. Για τον εξωτερικά παρατηρητή, πού βλέπει μέσα από ένα παράθυρο του ανελκυστήρα, το ρολόι και το μαντήλι πέφτουν ακριβώς με τον ίδιο τρόπο, με την ίδια επιτάχυνση, (δεδομένης της ισότητας της αδρανούς και της βαρείας μάζας). Η ισότητα των δυο μαζών ήταν, συμπωματική από την άποψη της κλασικής μηχανικής και δεν έπαιζε ρόλο στη δομή της. Εδώ όμως η ισότητα αυτή, που αντικαθρεφτίζεται στη ίση επιτάχυνση πτώσης όλων των σωμάτων, είναι ουσιώδης και αποτελεί τη βάση όλης της συλλογιστικής.

Ας ξαναρθούμε στο μαντήλι και στο ρολόι πού πέφτουν: για τον εξωτερικό παρατηρητή και τα δυο πέφτουν με την ίδια επιτάχυνση. Αλλά το ίδιο συμβαίνει και για τον ανελκυστήρα και η απόσταση ανάμεσα στο πάτωμα και τα δυο σώματα, δε θα μεταβληθεί. Για τον εσωτερικό παρατηρητή, τα δύο σώματα μένουν ακριβώς εκεί πού ήταν όταν τα άφησε ελεύθερα. Ο εσωτερικός παρατηρητής μπορεί να αγνοεί το πεδίο βαρύτητας, γιατί η πηγή του βρίσκεται έξω από το Σ.Σ. του. Βρίσκει πως καμιά δύναμη δε δρα πάνω στα δυο σώματα στο εσωτερικό του ανελκυστήρα σαν να βρίσκονταν σε αδρανειακό σύστημα. Αν ο παρατηρητής σπρώ­ξει ένα σώμα προς οποιαδήποτε κατεύθυνση, το σώμα θα κινείται ομαλά. Έτσι, οι νόμοι της κλασικής μηχανικής ισχύουν για τον εσωτερικό παρατηρητή. Όλα τα σώματα συμπεριφέρνονται σύμφωνα με την αρχή της αδράνειας. Το νέο Σ.Σ. μας, σταθερά δεμένο με τον ανελκυστήρα που πέφτει ελεύθερα, διαφέρει από το σύστημα αδράνειας μόνο από μια άποψη: Ο αδρανειακός χαρακτήρας του Σ.Σ. του ανελκυστήρα είναι περιορισμένος στο χώρο και στο χρόνο. Αργά ή γρήγορα το σώμα με την ομαλή κίνηση θα χτυπήσει σε μια πλευρά του ανελκυστήρα και η ομαλή του κίνηση θα καταστραφεί καθώς ο ανελκυστήρας θα συγκρουστεί με τη γη.

Ο τοπικός χαρακτήρας του Σ.Σ. έχει ουσιαστική σημασία. Αν ο φανταστικός ανελκυστήρας μας έφτανε από το βόρειο πόλο ως τον ισημερινό, κι αν αφήναμε να πέσει το μαντήλι πάνω από τον πόλο και το ρολόι πάνω από τον ισημερινό, τότε τα δυο σώματα δεν θα είχαν την ίδια επιτάχυνση για τον εξωτερικό παρατηρητή. Έτσι οι διαστάσεις του ανελκυστήρα πρέπει να είναι περιορισμένες, ώστε να μπορεί να θεωρηθεί ότι υφίσταται η ισότητα της επιτάχυνσης όλων των σωμάτων ως προς τον εξωτερικό παρατηρητή. 
Με αυτό τον περιορισμό, το Σ.Σ. έχει το χαρακτήρα συστήματος αδράνειας για τον εσωτερικό παρατηρητή. Αν φαντα­στούμε ένα άλλο Σ.Σ., έναν άλλον ανελκυστήρα που κινείται ομαλά ως προς τον ανελκυστήρα που πέφτει ελεύθερα, τότε αυτά τα δυο Σ.Σ. θα είναι τοπικά συστήματα αδράνειας. Όλοι οι νόμοι είναι οι ίδιοι και στα δύο και το πέρασμα από το ένα στο άλλο, δίνεται από τους μετασχηματισμούς του Lorentz. 
Ας δούμε τώρα με ποιο τρόπο περιγράφουν ό,τι συμβαίνει μέσα στον ανελκυστήρα οι δυο παρατηρητές: Ο εσωτερικός και ο εξωτερικός.

Ο εξωτερικός παρατηρητής σημειώνει την κίνηση του ανελκυστήρα καθώς και όλων των σωμάτων στα εσωτερικό του και τη βρίσκει σύμφωνη με τι νόμο της βαρύτητας του Νεύτωνα. Γι' αυτόν ή κίνηση δεν είναι ομαλή, αλλά επιταχυνόμενη, εξ αιτίας της δράσης του πεδίου βαρύτητας της γης.

Ωστόσο, κάποιος μέσα στον ανελκυστήρα, θα μπορούσε κάλλιστα να υποθέσει πως ο ανελκυστήρας του ηρεμεί και πως το σύστημα συντεταγμένων του είναι αδρανειακό.

Είναι αδύνατο να ρυθμίσουμε τη διαφορά των δυο παρατηρητών. Καθένας τους θα μπορούσε να διεκδικήσει το δικαίωμα να αναφέρει όλα τα γεγονότα στο Σ.Σ. του. Κι οι δυο περιγραφές θα μπορούσαν να έχουν την ίδια εσωτερική συνοχή.

Άρα λοιπόν είναι δυνατή μια συνεπής περιγραφή φυσικών φαινομένων σε δυο διαφορετικά Σ.Σ., ακόμα κι αν δεν κινούνται ομαλά το ένα ως προς το άλλο. Αλλά για μια τέτοια περιγραφή, πρέπει να λάβουμε υπ' όψη μας τη βαρύτητα, χτίζοντας κατά κάποιο τρόπο τη «γέφυρα» πού κάνει δυ­νατό το πέρασμα από το ένα Σ.Σ. στο άλλο. Το πεδίο βαρύτητας υπάρχει για τον εξωτερικό παρατηρητή· δεν υπάρχει όμως για τον εσωτερικό. Για τον εξωτερικό παρατηρητή υπάρχει η επιταχυνόμενη κίνηση του ανελκυστήρα μέσα στο πεδίο βαρύτητας, ενώ για τον εσωτερικό παρατηρητή υπάρχει ηρεμία και το πεδίο βαρύτητας είναι ανύπαρκτο. Αλλά η «γέφυρα», δηλαδή το πεδίο βαρύτητας πού κάνει δυνατή την περιγραφή στα δυο Σ.Σ., στηρίζεται πάνω στην ισοδυναμία της βαρείας και της αδρανούς μάζας. Χωρίς αυτήν, η σειρά των συλλογισμών που θέσαμε θα αποτύγχανε.

Ας φανταστούμε τώρα ένα αδρανειακό Σ.Σ., όπου ισχύει η αρχή της αδράνειας. Περιγράψαμε τι συμβαίνει σ' ένα ανελκυστήρα που βρίσκεται σ' ένα τέτοιο Σ.Σ. Τώρα αλλάζουμε την εικόνα μας. Κάποιος απ' έξω έδεσε ένα σχοινί στη στέγη του ανελκυστήρα και τραβάει με μια σταθερή δύναμη, προς την κατεύθυνση πού δείχνει το επόμενο σχήμα.

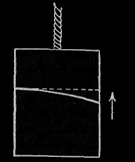
Εφ’ όσον οι νόμοι της μηχανικής ισχύουν σ' αυτό το Σ.Σ., ο ανελκυστήρας κινείται με σταθερή επιτάχυνση προς την κατεύθυνση της κίνησης. Ας ακούσουμε πάλι την εξήγηση πού δίνουν στα φαινόμενα που διαδραματίζονται μέσα στον ανελκυστήρα, ο εσωτερικός και ο εξωτερικός παρατηρητής.

Ο εξωτερικός παρατηρητής. Το Σ.Σ. μου είναι σύστημα αδράνειας. Ο ανελκυστήρας κινείται με σταθερή επιτάχυνση, εξ αιτίας της σταθερής δύναμης που δρα πάνω του. Ο εσωτερικός παρατη­ρητής βρίσκεται σε απόλυτη κίνηση. Γι' αυτόν δεν ισχύουν οι νόμοι της μηχανικής. Δεν βρίσκει ότι σώματα που δεν υφίστανται την επίδραση καμιάς δύναμης ηρεμούν. Αν αφήσει ένα σώμα να πέσει, χτυπάει αμέσως το πάτωμα του ανελκυστήρα, γιατί το πάτωμα επιταχύνεται προς το σώμα.

Ο εσωτερικός παρατηρητής. Ο ανελκυστήρας μου δεν βρίσκεται σε απόλυτη κίνηση.  Παραδέχομαι πώς το Σ.Σ. μου, που είναι σταθερά δεμένο με τον ανελκυστήρα, δεν είναι πραγματικά σύστημα αδράνειας, αλλά αυτό δεν έχει σχέση με την απόλυτη κίνηση. Τα σώματα πέφτουν, γιατί ο ανελκυστήρας μου βρίσκεται μέσα σε ένα πεδίο βαρύτητας. Παρατηρώ ακριβώς τα ίδια είδη κινήσεων με έναν άνθρωπο πάνω στη γη.

Αυτές οι δυο περιγραφές έχουν λογική συνοχή και δεν υπάρχει δυνατότητα να αποφασίσει κανείς, ποια είναι αληθινή.

Υπάρχει άραγε τρόπος να βγει κανείς από το διφορούμενο των δυο περιγραφών και να αποφασίσει υπέρ της μιας απορρίπτοντας την άλλη; Ας υποθέσουμε πως μια φωτεινή ακτίνα εισέρχεται οριζόντια από ένα παράθυρο στον ανελκυστήρα και χτυπά στην απέναντι πλευρά, υστέρα από ένα συντομότατο χρονικό διάστημα. Ας δούμε τώρα πώς θα μπορούσε να προβλεφθεί από τους δυο παρατηρητές η τροχιά της φωτεινής ακτίνας.

Ο εξωτερικός παρατηρητής, πιστεύει πως ο ανελκυστήρας επιταχύνεται θα σκεφτόταν ως εξής: Η φωτεινή ακτίνα μπαίνει οριζόντια από το παράθυρο και κινείται ευθύγραμμα, με σταθερή ταχύτητα, προς την απέναντι πλευρά. Αλλά ο ανελκυστήρας κινείται προς τα πάνω και αλλάζει θέση την ώρα που η ακτίνα κινείται προς την πλευρά του. Η ακτίνα λοιπόν θα χτυπήσει ένα σημείο που δεν είναι ακριβώς απέναντι από το σημείο της εισόδου, αλλά λίγο πιο κάτω. Η διαφορά θα είναι ελάχιστη, ωστόσο θα υπάρχει, και η φωτεινή ακτίνα προχωρεί ως προς τον ανελκυστήρα όχι ευθύγραμμα, αλλά σε ελαφριά καμπύλη τροχιά. Η διαφορά οφείλεται στην απόσταση που διατρέχει ο ανελκυστήρας, ώσπου η ακτίνα να διανύσει το εσωτερικό του.

Ο εσωτερικός παρατηρητής, πιστεύει στην ύπαρξη πεδίου βαρύτητας που δρα σ' όλα τα αντικείμενα. Θα έλεγε πως δεν υπάρχει επιταχυνόμενη κίνηση του ανελκυστήρα. Υπάρχει μονάχα η δράση του πεδίου βαρύτητας. Αν θεωρούσε ότι μια φωτεινή ακτίνα δεν έχει βάρος και ότι δε θα επηρεαστεί από το πεδίο βαρύτητας, θα συμπέρανε ότι αν αυτή εισέλθει οριζόντια, θα χτυπήσει την πλευρά σε ένα σημείο, ακριβώς απέναντι από το σημείο εισόδου.

Από αυτά θα φαινόταν πως υπάρχει δυνατότητα να αποφασίσουμε ανάμεσα σ' αυτές τις δυο απόψεις, μια και το φαινόμενο θα μπορούσε να είναι διαφορετικό για τους δυο παρατηρητές. Αλλά υπάρχει ένα σοβαρό λάθος στη σκέψη του εσωτερικού παρατηρητή που σώζει το προηγούμενο συμπέρασμα: Μια φωτεινή ακτίνα μεταφέρει ενέργεια. Η ενέργεια έχει μάζα και κάθε αδρανής μάζα έλκεται από το πεδίο βαρύτητας, μια και η αδρανής και η βαρεία μάζα είναι ισοδύναμες. Μια φωτεινή ακτίνα θα καμπυλωθεί μέσα σ' ένα πεδίο βαρύτητας, ακριβώς όπως ένα σώμα που θα εκτοξευόταν οριζόντια με την ταχύτητα του φωτός. 
Από τα παραδείγματα αυτά συνάγεται ότι είναι βάσιμη η ελπίδα να διατυπώσουμε μια σχετικιστική φυσική. Αλλά για να το κάνουμε, πρέπει πρώτα να πραγματευτούμε το πρόβλημα της βαρύτητας.

Η απόλυτη κίνηση και τα συστήματα αδράνειας μπορούν να εξαλειφθούν από τη φυσική, και μπορεί να διαμορφωθεί μια νέα σχετικιστική φυσική. Τα ιδεατά πειράματα που αναπτύξαμε φανερώνουν με ποιο τρόπο συνδέονται στενά το πρόβλημα της γενικής θεωρίας της σχετικότητας και το πρόβλημα της βαρύτητας, και γιατί η ισοδυναμία της βαρείας και της αδρανούς μάζας είναι τόσο ουσιαστική γι' αυτή τη σύνδεση. Οι νόμοι της βαρύτητας, όπως όλοι οι νόμοι της φύσης, πρέπει να διατυπωθούν για όλα τα δυνατά Σ.Σ., ενώ οι νόμοι της κλασικής μηχανικής, όπως διατυπώθηκαν από τον Νεύτωνα, ισχύουν μόνο στα συστήματα αδράνειας.

6) Η καμπύλωση του χωροχρόνου

Θα πλησιάσουμε τώρα το ζήτημα της σύνδεσης ανάμεσα στη γενική θεωρία της σχετικότητας και τη γεωμετρία. Ας αρχίσουμε με την περιγραφή ενός επίπεδου δισδιάστατου κόσμου όπου ζουν μονάχα όντα δυο διαστάσεων τα οποία μπορούν να σκέφτονται και να παράγουν επιστήμη. Τα όντα αυτά είναι ανίκανα να φανταστούν έναν τρισδιάστατο χώρο, ακριβώς όπως εμείς είμαστε ανίκανοι να φανταστούμε ένα τετραδιάστατο. Μπορούμε να θλάσουμε και να καμπυλώσουμε γραμμές και επιφάνειες, δύσκολα όμως μπορούμε να φανταστούμε ένα τρισδιάστατο χώρο τεθλασμένο και καμπύλο.

Τα όντα αυτά θα μπορούσαν να αναπτύξουν τέλεια την ευκλείδεια επιπεδομετρία.

Ας φανταστούμε τώρα πώς τα δισδιάστατα αυτά όντα ζουν σε διαφορετικές συνθήκες. Ας φανταστούμε πώς κάποιος απ' έξω, από την «τρίτη διάσταση», τα μεταφέρει στην επιφάνεια μιας γιγάντιας σφαίρας. Αν τα οντά είναι πολύ μικρά σε σχέση με τη συνολική επιφάνεια, αν δεν έχουν κανένα μέσον τηλεπικοινωνίας κι αν δε μπορούν να πάνε πολύ μακριά, δε θα νιώσουν καμιά αλλαγή. Π.χ. σε δυο μικρούς, ομόκεντρους κύ­κλους, ο λόγος των περιφερειών είναι πάντα ίση με το λόγο των ακτινών. Ταξιδεύοντας σε ευθεία γραμμή, δεν θα ξαναρθούν ποτέ στο σημείο απ' όπου ξεκίνησαν.

Αλλά αν τα όντα αυτά αναπτύξουν στην πορεία του χρόνου τις θεωρητικές και τεχνικές γνώσεις τους και εφεύρουν μέσα επικοινωνίας που τους επιτρέπουν να διατρέχουν γρήγορα μεγάλες αποστάσεις, θα παρατηρήσουν τότε, πως πηγαίνοντας ίσια μπροστά, θα επιστρέφουν τελικά την αφετηρία τους. «Ίσια μπροστά» σημαίνει κατά μήκος ενός μέγιστου κύκλου της σφαίρας. Θα παρατηρήσουν επίσης πώς η σχέση των περιφε­ρειών δυο ομόκεντρων κύκλων δεν είναι ίση με τη σχέση των ακτινών τους, αν ο ένας από τους κύκλους είναι μικρός και ο άλλος μεγάλος.

Θα καταλάβουν τελικά πώς ο κόσμος τους είναι πεπερασμένος και πως κυβερνιέται από γεωμετρικές αρχές διαφορετικές από εκείνες που μάθανε. Ότι κόσμος τους είναι μια σφαιρική επιφάνεια με δυο διαστάσεις. Θα βαλθούνε να μάθουν νέες αρχές γεωμετρίας για τον δισδιάστατο χώρο τους, που αν και θα διαφέρουν τελείως από του Ευκλείδη, θα μπορούν να δια­τυπωθούν με την ίδια εσωτερική ενότητα και λογική.

Ας ξαναρθούμε τώρα στα τρισδιάστατα όντα του κόσμου μας. Ας φανταστούμε πως παρατηρήθηκαν ασυμφωνίες με την ευκλείδεια γεωμετρία, πως το άθροισμα π.χ. των γωνιών ενός μεγάλου τριγώνου, κατασκευασμένου με σταθερές ράβδους δεν είναι ίσο με δυο ορθές γωνίες. Θα έπρεπε να εγκαταλείψουμε την ιδέα πως ο χώρος μας είναι ευκλείδειος και να ζητήσουμε μία πιο πειστική εικόνα της πραγματικότητας.

Η ανάγκη αυτή μπορεί να φανεί με ένα ιδεατό πείραμα, που δείχνει πώς μια πραγματικά ρελατιβιστική φυσική, δεν μπορεί να θεμελιωθεί στην ευκλείδεια γεωμετρία.

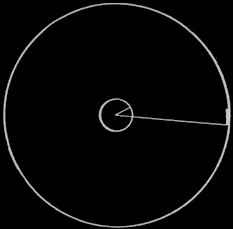
Ας φανταστούμε ένα μεγάλο δίσκο που πάνω του είναι χαραγμένοι δυο ομόκεντροι κύκλοι, ο ένας πολύ μικρός κι ο άλλος πολύ μεγάλος, και που το κοινό κέντρο τους συμπίπτει με το κέντρο του δίσκου. Ο δίσκος στρέφεται γρήγορα σχετικά με έναν εξωτερικά παρατηρητή (ο άξονας γύρω από τον όποιο στρέφεται ο δίσκος περνάει από το κέντρο του). Πάνω του στέκεται ένας εσωτερικός παρατηρητής. Υποθέτουμε ακόμα πως το Σ.Σ. του εξωτερικού παρατηρητή είναι σύστημα αδράνειας. Ο εξωτερικός παρατηρητής μπορεί να χαράξει στο Σ.Σ. του δυο κύκλους ίδιου μεγέθους με τους κύκλους του στρεφόμενου δίσκου.

Η ευκλείδεια γεωμετρία ισχύει στο Σ.Σ. του, μια και είναι σύστημα αδράνειας. Έτσι θα βρει πως ο λόγος των περιφερειών είναι ίσος με το λόγο των ακτινών. Τι γίνεται όμως με τον παρατηρητή πάνω στα δίσκο; Από την άποψη της κλασικής φυσικής, αλλά και της ειδικής θεωρίας της σχετικότητας, το Σ.Σ. του είναι απαγορευμένο. Αλλά αν έχουμε την πρόθεση να βρούμε νέους τύπους για τους νόμους της φυσικής που να ισχύουν σε οποιοδήποτε Σ.Σ., οφείλουμε να πάρουμε το ίδιο στα σοβαρά, τόσο τον παρατηρητή πάνω στα δίσκο, όσο και τον εξωτερικό παρατηρητή. Απ' έξω, κοιτάμε τον εσωτερικό παρατηρητή, που προσπαθεί να μετρήσει το μήκος των περιφερειών και των ακτινών πάνω στον περιστρεφόμενο δίσκο. Χρησιμοποιεί τον ίδιο κανόνα με τον εξωτερικό παρατηρητή. «Τον ίδιο» σημαίνει, ή πραγματικά τον ίδιο κανόνα που ο εξωτερικός παρατηρητής δίνει στον παρατηρητή του δίσκου, ή τον ένα από δυο κανόνες που έχουν το ίδιο μήκος όταν βρίσκονται σε ηρεμία σε ένα Σ.Σ.

Ο εσωτερικός παρατηρητής πάνω στο δίσκο αρχίζει να μετράει την ακτίνα και την περιφέρεια του μικρού κύκλου. Τα μέρη του δίσκου κοντά στο κέντρο έχουν πολύ μικρές ταχύτητες. Αν ο κύκλος είναι πολύ μικρός, ο κανόνας έχει το ίδιο μήκος για τον εξωτερικό και για τον εσωτερικό παρατηρητή και το αποτέλεσμα των μετρήσεων τους θα 'ναι το ίδιο και για τους δυο. Ο παρατηρητής πάνω στο δίσκο, μετράει τώρα την ακτίνα του μεγάλου κύκλου. Ο κανόνας τοποθετημένος πάνω στην ακτίνα, βρίσκεται σε κίνηση ως προς τον εξωτερικό παρατηρητή. Ένας τέτοιος κανόνας δεν θα υποστεί συστολή γιατί η διεύθυνση της κίνησης είναι κάθετη προς τον κανόνα. Τρεις μετρήσεις λοιπόν, δηλαδή των δυο ακτινών και της μικρής περιφέ­ρειας, είναι ίδιες και για τους δυο παρατηρητές. Αλλά δεν συμβαίνει το ίδιο και με την τέταρτη μέτρηση. Το μήκος της μεγάλης περιφέρειας θα είναι διαφορετικό για τους δυο παρατηρητές. Ο κανόνας πού είναι τοποθετημένος πάνω στην περιφέρεια, κατά την κατεύθυνση της κίνησης, θα φαίνεται πιο κοντός για τον εξωτερικό παρατηρητή, αν τον συγκρίνει με τον ακίνητο κανόνα του. Η τα­χύτητα του μεγάλου κύκλου είναι πολύ πιο μεγάλη από του μικρού και η συστολή πρέπει να ληφθεί υπ' όψη. Αν λοιπόν εφαρμόσουμε τα αποτελέσματα της ειδικής θεωρίας της σχετικότητας, το συμπέρασμα μας θα είναι ότι το μήκος της μεγάλης περιφέρειας, μετρούμενο από τους δυο παρατηρητές, πρέπει να είναι διαφορετικό. Έτσι ο λόγος των δυο ακτίνων δεν είναι ίσος με τον λόγο των δυο περιφερειών για τον παρατηρητή του δίσκου, όπως είναι για τον εξωτερικό παρατηρητή! Ο παρατηρητής πάνω στο δίσκο, δεν μπορεί να επιβεβαιώσει την ισχύ της ευκλείδειας γεωμετρίας στο Σ.Σ. του.

Αφού έφτασε σ' αυτό το συμπέρασμα ό παρατηρητής πάνω στο δίσκο, θα μπορούσε να πει πως δεν επιθυμεί να έχει ένα Σ.Σ. οπού δεν ισχύει η ευκλείδεια γεωμετρία. Η κατάρρευση της ευκλεί­δειας γεωμετρίας οφείλεται στην απόλυτη περιστροφή, στο γεγονός πώς το Σ.Σ. του είναι απαγορευμένο. Όταν όμως σκέφ­τεται μ' αυτό τον τρόπο, ό παρατηρητής απορρίπτει τη βασική ιδέα της γενικής θεωρίας της σχετικότητας. Αν όμως θέλουμε να απορρίψουμε την απόλυτη κίνηση και να διατηρή­σουμε την ιδέα της γενικής θεωρίας της σχετικότητας, πρέπει να οικοδομήσουμε τη φυσική πάνω στη βάση μιας γεωμετρίας γενικότερης από του Ευκλείδη. Δεν υπάρχει τρόπος να ξεφύγουμε απ' αυτή τη συνέπεια, αν όλα τα Σ.Σ. είναι επιτρεπτά.

Οι μεταβολές που επέφερε η γενική θεωρία της σχετικότητας, δεν περιορίζονται μονάχα στο χώρο. Στην ειδική θεωρία της σχετικότητας είχαμε ρολόγια που ηρεμούσαν σε κάθε Σ.Σ., που είχαν τον ίδιο ρυθμό, και που ήταν συγχρονισμένα - έδειχναν δηλαδή την ίδια ώρα. Τι γίνεται με ένα ρολόι σ' ένα Σ.Σ. πού δεν είναι σύστημα αδράνειας; Θα χρησιμοποιήσουμε πάλι το ιδεατό πείραμα με τον περιστρεφόμενο δίσκο. Ο εξωτερικός παρατηρητής έχει στο σύστημα αδράνειας του τέλεια ρολόγια, που προχωρούν όλα με τον ίδιο ρυθμό και είναι συγχρονισμένα. Ο παρατηρητής πάνω στο δίσκο παίρνει δυο όμοια ρολόγια και τα τοποθετεί, το ένα πάνω στη μικρή περιφέρεια, και τ' άλλο πάνω στη μεγάλη. Το ρολόι πάνω στη μικρή περιφέρεια έχει πολύ μικρή ταχύτητα σε σχέση με τον εξωτερικά παρατηρητή. Μπορούμε λοιπόν να συμπεράνουμε πως ο ρυθμός του θα είναι ίδιος με του εξωτερικού ρολογιού. Αλλά το ρολόι που είναι τοποθετημένο πάνω στη με­γάλη περιφέρεια, έχει μια σημαντική ταχύτητα κι αυτό κάνει να αλλάζει ο ρυθμός του ως προς τα ρολόγια του εξωτερικού παρατη­ρητή και κατά συνέπεια και ως προς το ρολόι που είναι πάνω στη μικρή περιφέρεια. Τα δυο περιστρεφόμενα ρολόγια θα 'χουν λοιπόν διαφορετικό ρυθμό. Εφαρμόζοντας τα αποτελέσματα της ειδικής θεωρίας της σχετικότητας, βλέπουμε πάλι πως στο περιστρεφόμενο Σ.Σ. δεν μπορούμε να κάνουμε διευθετήσεις όμοιες μ' αυτές πού γίνονται σ' ένα σύστημα αδράνειας.

Ας δούμε και μια άλλη παράμετρο του προβλήματος: Ο εσωτερικός παρατηρητής νιώθει μια δύναμη να τον τραβάει από το κέντρο προς την περιφέρεια. Αλλά θεωρεί υπεύθυνο γι' αυτό ένα παράξενο πεδίο βαρύ­τητας που κατευθύνεται προς το εξωτερικό του δίσκου, παραμορφώνει τις σταθερές ράβδους και μεταβάλλει τα ρυθμό των ρολογιών του. Για αυτόν, το πεδίο βαρύτητας, η μη ευκλείδεια γεωμετρία και τα ρολόγια με διαφορετικούς ρυθμούς συνδέονται στενά μεταξύ τους. Όταν δεχόμαστε ένα οποιοδήποτε Σ.Σ., οφείλουμε ταυτόχρονα να δεχόμαστε και την ύπαρξη ενός κατάλληλου πεδίου βαρύτητας, και την επίδραση του στις σταθερές ράβδους και τα ρολόγια.

Στη γενική θεωρία της σχετικότητας δεν μπορούμε να χρησιμοποιήσουμε δομή με τους παράλληλους και κάθετους κανόνες και τα συγχρονισμένα ρολόγια, όπως στην ειδική θεωρία της σχετικότητας. Σε ένα αυθαίρετο Σ.Σ. δεν μπορούμε να καθορίσουμε το σημείο και τη χρονική στιγμή ενός γεγονότος, με τη βοήθεια σταθερών κανόνων και ρυθμικών, συγχρονισμένων ρολογιών, όπως στο σύστημα αδράνειας της ειδικής θεωρίας της σχετικότητας. Μπορούμε πάντα να διευθετούμε τα γεγονότα με τη βοήθεια των μη ευκλείδειων κανόνων μας και των ρολογιών που ο ρυθμός τους αλλάζει. Αλλά πραγματικές μετρήσεις, που απαιτούν σταθερούς κανόνες και τέλεια ρυθμικά και συγχρονισμένα ρολόγια, δεν μπορούν να πραγματοποιηθούν παρά σε τοπικά συστήματα αδράνειας. Γι' αυτό ισχύει ολόκληρη η ειδική θεωρία της σχετικότητας, αλλά το «καλό» μας Σ.Σ. είναι μόνο τοπικό, γιατί ο χαρακτήρας του σαν συστήματος αδράνειας, είναι περιορισμένος τοπικά και χρονικά. Ακόμα και στο αυθαίρετο Σ.Σ. μας, μπορούμε να προβλέψουμε τα αποτελέσματα των μετρήσεων πού πραγματοποιούνται στο τοπικό σύστημα αδράνειας. Αλλά για να γίνει αυτό, πρέπει να ξέρουμε το γεωμετρικό χαρακτήρα του χωροχρονικού συνεχούς.  

Τα ιδεατά μας πειράματα αποκαλύπτουν το γενικό χαρακτήρα της νέας σχετικιστικής φυσικής. Μας δείχνουν ότι το θεμελιώδες πρόβλημα είναι το πρόβλημα της βαρύτητας. Δείχνουν ακόμα πως η γενική θεωρία της σχετικότητας οδηγεί σε μια γενίκευση των εννοιών του χώρου και του χρόνου.

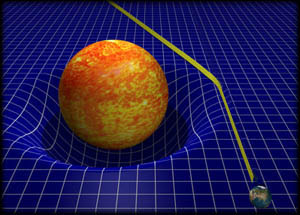
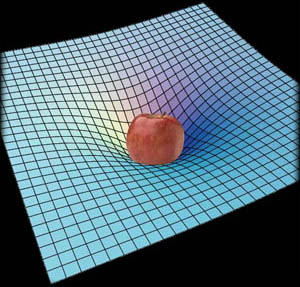
Συμπερασματικά, λοιπόν, ο χωροχρόνος έχει την ιδιότητα να καμπυλώνεται παρουσία ύλης όπως καμπυλώνεται ένα τεντωμένο σεντόνι όταν τοποθετήσουμε πάνω του μια μπάλα. Αν εκτοξεύσουμε τώρα μια μικρή μπίλια πάνω στην επιφάνεια του σεντονιού τότε η τροχιά που θα διαγράψει η μπίλια προφανώς δεν θα είναι ευθύγραμμη αλλά καμπύλη. Η καμπύλωση της τροχιάς δεν οφείλεται στη βαρυτική έλξη που ασκεί η μπάλα στην μικρή μπίλια αλλά στην παραμόρφωση που προκάλεσε η μπάλα στην επιφάνεια του σεντονιού. Με τον ίδιο τρόπο μια μεγάλη μάζα (π.χ. ένα αστέρι) καμπυλώνει το χωροχρόνο γύρω της στο Σύμπαν. Έτσι όλα τα ουράνια σώματα δεν αναγκάζονται να κινούνται σε καμπύλες τροχιές λόγω της δύναμης που λέγεται βαρύτητα, αλλά ακολουθούν τις καμπύλες γραμμές του παραμορφωμένου χωροχρόνου. Όπως πολύ ωραία το έθεσε ένας μεγάλος φυσικός: «Η ύλη λέει στο χώρο πώς να καμπυλωθεί και ο χώρος λέει στην ύλη πώς να κινηθεί».

dimitris.webgalaxy.gr
#parallelquantum